Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
Tags
- 파이썬 시각화
- 매틀랩
- SQL
- 블로그
- Python
- Blog
- 딥러닝
- 독후감
- Linux
- python visualization
- 통계학
- 한빛미디어
- 리눅스
- MySQL
- 파이썬
- 서평단
- matplotlib
- 텐서플로
- Google Analytics
- Visualization
- 티스토리
- Pandas
- 월간결산
- tensorflow
- Ga
- 한빛미디어서평단
- 시각화
- MATLAB
- Tistory
- 서평
Archives
- Today
- Total
pbj0812의 코딩 일기
[통계학] python을 통한 제곱합(SS), 제곱평균(MS), 처리간 제곱합(SSB), 처리내 제곱합(SSE), 총제곱합(SST) 본문
Science/통계학
[통계학] python을 통한 제곱합(SS), 제곱평균(MS), 처리간 제곱합(SSB), 처리내 제곱합(SSE), 총제곱합(SST)
pbj0812 2020. 10. 3. 01:230. 목표
- python을 통한 제곱합(SS), 제곱평균(MS), 처리간 제곱합(SSB), 처리내 제곱합(SSE), 총제곱합(SST) 구현
1. 기본 이론
1) 제곱합(Sum of Squares)
- 관측값과 평균의 차이를 제곱하여 더해준 값, 변동(variation)
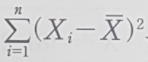
2) 제곱평균(Mean Squre)
- 제곱합을 자유도로 나누어 준 값, 분산
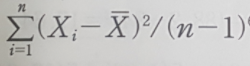
3) 처리간 제곱합(Sum of Squares Between Treatments)
- 각 처리평균 간의 차이를 측정

4) 처리내 제곱합(Sum of Squares due to Error)
- 개별 관측값이 각 처리 평균으로부터 떨어진 차이를 측정
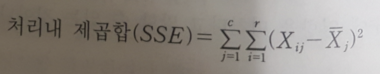

5) 총제곱합(Sum of Squares Total)
- 개별관측값이 총평균으로부터 떨어진 차이를 측정
- 총 제곱합 = 처리간 제곱합 + 처리내 제곱합
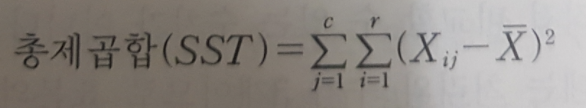
2. 실습
1) library 호출
import pandas as pd
import numpy as np2) 데이터 생성
df = pd.DataFrame({"A":[77, 79, 87, 85, 78], "B":[80, 82, 86, 85, 80], "C":[83, 91, 94, 88, 85]})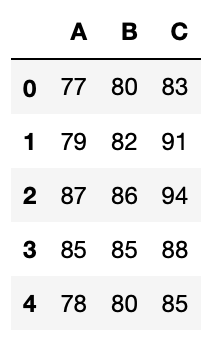
3) 평균 모듈
def mean(inp):
result = 0
len_inp = len(inp)
for i in inp:
result += i
result = result / len_inp
return result- 테스트
result_mean = mean(df2[:, 0])
print(result_mean)- 결과
81.24) 제곱합(SS) 모듈
# inp은 dataframe 형태
def SS(inp):
inp2 = np.array(inp)
inp_shape = df2.shape
result = []
for i in range(inp_shape[1]):
tmp_list = inp2[:, i]
tmp_mean = mean(tmp_list)
tmp = []
for j in tmp_list:
tmp.append((j - tmp_mean) ** 2)
result.append(sum(tmp))
return result- 테스트
result_SS = SS(df)
print(result_SS)- 결과
[80.80000000000001, 31.199999999999996, 78.80000000000001]5) 제곱평균(MS) 모듈
- np.shape로 행렬의 사이즈를 받음
- 첫 번째 for에서는 각 열의 평균을 연산
- 두번째 for에서는 각 데이터 마다의 값들을 연산
# inp은 dataframe 형태
def MS(inp):
inp2 = np.array(inp)
inp_shape = df2.shape
result = []
for i in range(inp_shape[1]):
tmp_list = inp2[:, i]
tmp_mean = mean(tmp_list)
tmp = []
for j in tmp_list:
tmp.append((j - tmp_mean) ** 2)
tmp = sum(np.array(tmp) / (inp_shape[0] - 1))
result.append(tmp)
return result- 테스트
result_MS = MS(df)
print(result_MS)- 결과
[20.200000000000003, 7.799999999999999, 19.700000000000003]6) 처리간 제곱합(SSB) 모듈
- SS에서 두 번째 for를 없애고 그 대신 관측값의 개수(inp_shape[0])를 곱해줌
# inp은 dataframe 형태
def SSB(inp):
inp2 = np.array(inp)
inp_shape = df2.shape
# 전체평균
total_mean = mean(df2.reshape(inp_shape[0] * inp_shape[1], 1))[0]
result = []
for i in range(inp_shape[1]):
tmp_list = inp2[:, i]
tmp_mean = mean(tmp_list)
tmp = inp_shape[0] * ((tmp_mean - total_mean) ** 2)
result.append(tmp)
return sum(result)- 테스트
result_SSB = SSB(df)
print(result_SSB)- 결과
137.200000000000137) 처리내 제곱합(SSE) 모듈
# inp은 dataframe 형태
def SSE(inp):
inp2 = np.array(inp)
inp_shape = df2.shape
result = []
for i in range(inp_shape[1]):
tmp_list = inp2[:, i]
tmp_mean = mean(tmp_list)
tmp2 = 0
for j in tmp_list:
tmp = (j - tmp_mean) ** 2
tmp2 += tmp
result.append(tmp2)
return sum(result)- 테스트
result_SSE = SSE(df)
print(result_SSE)- 결과
190.88) 총제곱합(SST) 모듈
# inp은 dataframe 형태
def SST(inp):
inp2 = np.array(inp)
inp_shape = df2.shape
# 전체평균
total_mean = mean(df2.reshape(inp_shape[0] * inp_shape[1], 1))[0]
result = []
for i in range(inp_shape[1]):
tmp_list = inp2[:, i]
tmp_mean = mean(tmp_list)
tmp2 = 0
for j in tmp_list:
tmp = (j - total_mean) ** 2
tmp2 += tmp
result.append(tmp2)
return sum(result)- 테스트
result_SST = SST(df)
print(result_SST)- 결과
328.03. 참고
'Science > 통계학' 카테고리의 다른 글
| [통계학] PYTHON을 이용한 RMSE, MAPE 구현 및 데이터에 따른 결과 비교 (0) | 2020.11.02 |
|---|---|
| [통계학] python을 이용한 최소제곱법과 경사하강법 구현 (0) | 2020.10.04 |
| [통계학] python을 통한 체계적 표본추출 구현 (0) | 2020.09.18 |
| [통계학] python을 이용한 단순무작위표본추출 (0) | 2020.09.10 |
| [통계학] python을 이용한 귀무가설의 판정 (0) | 2020.09.09 |
Comments



