| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- 한빛미디어서평단
- 파이썬 시각화
- 파이썬
- 블로그
- Pandas
- MySQL
- Google Analytics
- 텐서플로
- Visualization
- 통계학
- 티스토리
- 매틀랩
- tensorflow
- 딥러닝
- 서평
- Ga
- SQL
- matplotlib
- Blog
- 시각화
- Linux
- 월간결산
- python visualization
- 리눅스
- Python
- 독후감
- 서평단
- 한빛미디어
- Tistory
- MATLAB
- Today
- Total
pbj0812의 코딩 일기
[PYTORCH] 01_pytorch with examples (numpy) 본문
Pytorch with examples (numpy) 코드 분석
- 아래 글은 파이토치 튜토리얼 중 numpy 부분을 학습하여 영상으로 만든 것을 재구성한 글입니다.
원본링크 : https://pytorch.org/tutorials/beginner/pytorch_with_examples.html
유투브 영상 : https://youtu.be/ovENuzUM_5k
한글 주석 코드: https://github.com/pbj0812/deep_learning/blob/master/pytorch_tutorial/learning_pytorch_with_examples
코드 프리뷰
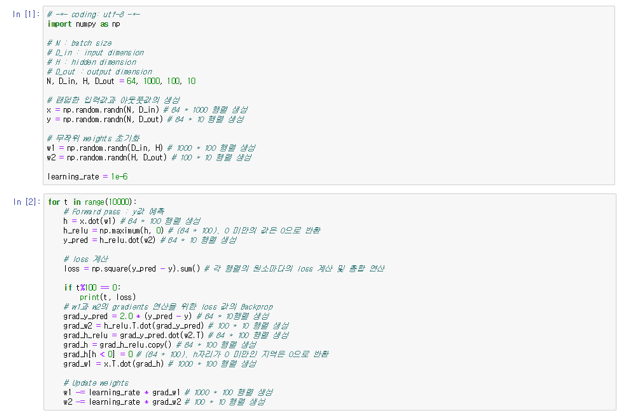
- 전체 코드이다.
- 비교적 짧게 구성되어 있다.
설계도

- 위 코드를 프리뷰하여 작성한 설계도이다.
- hidden layer 하나로 구성되어 있다.
Hyper parameter setting
N, D_in, H, D_out = 64, 1000, 100, 10
learning_rate = 1e-6
x = np.random.randn(N, D_in)
y = np.random.randn(N, D_out)
w1 = np.random.randn(D_in, H)
w2 = np.random.randn(H, D_out)
- 하이퍼 파라미터 세팅 부분이다.
- np.random.randn 함수를 이용하여 각 행렬을 실수로 채웠다.
hidden layer 생성
h = x.dot(w1)
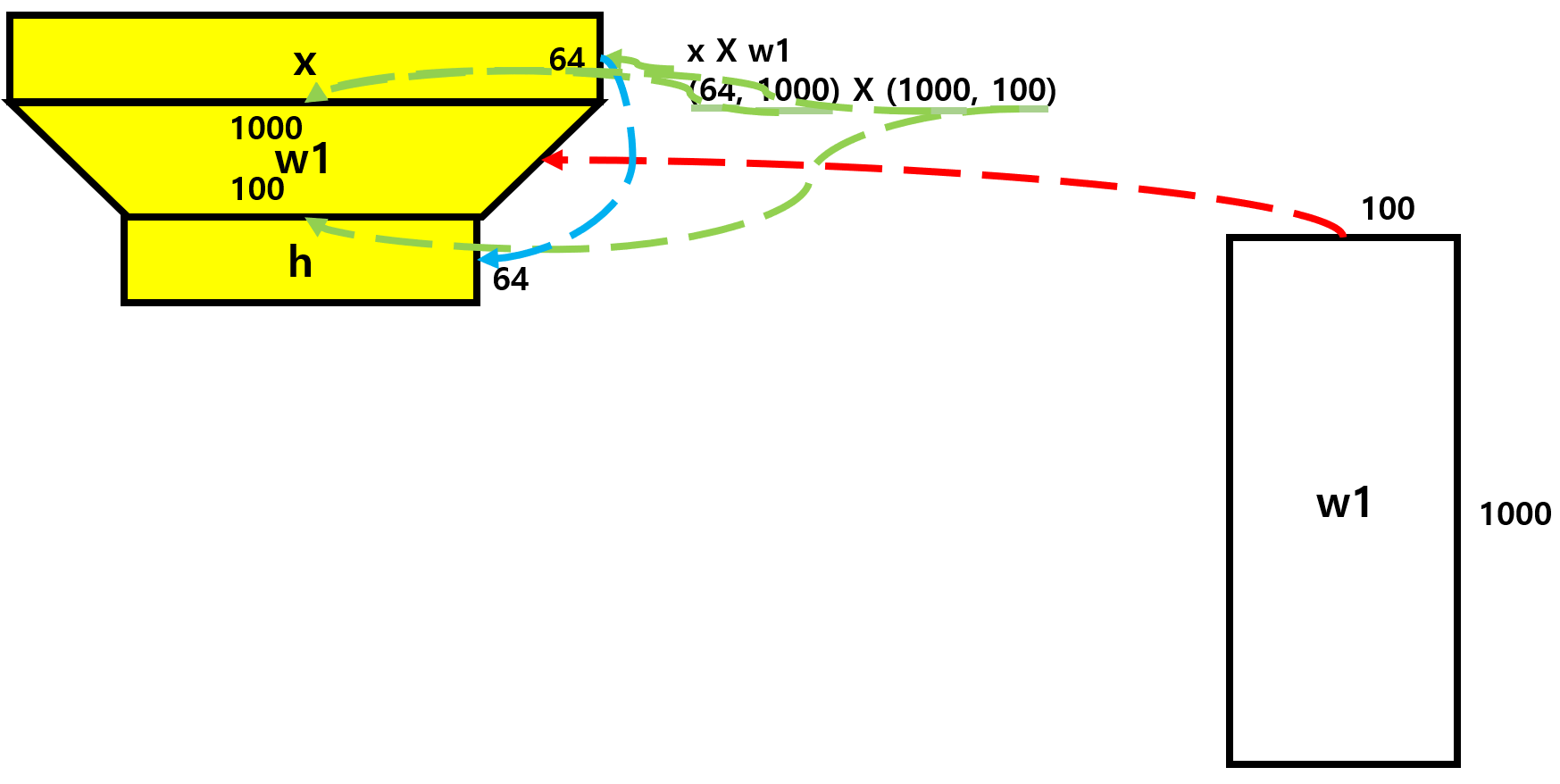
- x와 w1을 곱하여 hidden layer를 구현하였다.
- 이때 w1의 행의 갯수는 입력값의 수가 되고, 열의 갯수는 출력값의 갯수로 표현하기 위해 사다리꼴로 만들었다.
ReLU 구현
h_relu = np.maximum(h, 0)

- np.maximum 함수를 이용하여 ReLU를 구현하였다.
- ReLU는 오른쪽 그림에서 예를 들면 0보다 작은 입력값은 0으로 만들어 버리는 함수로 필요없는 가중치를 지워버린다고 할 수 있다.
예측값 출력
y_pred = h_relu.dot(w2)

- hidden layer와 w2를 곱하여 예측값을 만들었다.
loss function
loss = np.square(y_pred - y).sum()

- loss function으로 (예측값-실제값)^2의 방식을 취하였다.
- 이렇게 제곱을 한 이유로는 두 가지를 들 수 있겠다.
1. loss를 늘리기 위해서이다.
2. 단순히 loss function을 (예측값-실제값)으로 정하게 되면 합하게 될 때 오른쪽 그림과 같은 일이 발생하기 때문으로 보인다.
1) 오른쪽 그림에서 초록색 직선은 실제값, 노란색 동그라미는 예측값을 나타낸다.
2) 오른쪽 위 그림에서 loss는 0이라고 할 수 있다.
3) 오른쪽 아래 그림에서 각 지점에서 loss는 0이 아니지만 다 더하게 되면 0이 된다.
loss function 미분
grad_y_pred = 2.0 * (y_pred - y)

- (예측값-실제값)^2 의 미분값을 구현한 코드이다.
w2 가중치 구현
grad_w2 = h_relu.T.dot(grad_y_pred)

- w2의 가중치를 구현한 코드이다.
- 역산해서 올라가야하기 때문에 전에 만들었던 grad_y_pred 값과 h_relu의 값을 이용하여 만들었다.
- h_relu X w2 = y_pred이기 때문에 w2의 가중치를 구하기 위해서 h_relu를 90도 회전시켰다.
hidden layer의 가중치 구현
grad_h_relu = grad_y_pred.dot(w2.T)

- 전과 마찬가지의 방식으로 hidden layer의 가중치를 구현한다.
ReLU 구현
grad_h = grad_h_relu.copy()
grad_h[h < 0] = 0

- 처음의 h 부분에서 0 이하의 수가 있던 위치를 구하여 0으로 반환시켰다.
w1의 가중치 구현
grad_w1 = x.T.dot(grad_h)

- 위의 방식과 마찬가지로 역산하여 w1의 가중치를 구하였다.
weight 갱신
w1 -= learning_rate * grad_w1
w2 -= learning_rate * grad_w2

- 처음에 지정한 learning rate를 w1, w2의 가중치에 곱해준 뒤 w1, w2에서 제하였다.
- 부호가 -인 이유는 loss를 감소시키는 방향으로 진행되어야 하기 때문이다.
'인공지능 & 머신러닝 > PYTORCH' 카테고리의 다른 글
| [PYTORCH] 06_pytorch with examples (nn module) (0) | 2019.06.16 |
|---|---|
| [PYTORCH] 05_pytorch with examples (TensorFlow) (0) | 2019.06.16 |
| [PYTORCH] 04_pytorch with examples (autograd 재정의) (0) | 2019.06.10 |
| [PYTORCH] 03_pytorch with examples (autograd) (0) | 2019.05.31 |
| [PYTORCH] 02_pytorch with examples (tensor) (0) | 2019.05.29 |




