Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- 한빛미디어서평단
- 파이썬 시각화
- 서평단
- Visualization
- tensorflow
- 한빛미디어
- 시각화
- python visualization
- 월간결산
- 파이썬
- Tistory
- 텐서플로
- SQL
- Blog
- 티스토리
- 서평
- 통계학
- MATLAB
- Pandas
- 블로그
- 리눅스
- Google Analytics
- matplotlib
- Ga
- 딥러닝
- 매틀랩
- MySQL
- Linux
- Python
- 독후감
Archives
- Today
- Total
pbj0812의 코딩 일기
[통계학] spicy 패키지를 이용한 동전 던지기(베이지안) 본문
0. 목표
- scipy 패키지를 이용한 동전 던지기
1. 실습
1) library 호출
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
from IPython.core.pylabtools import figsize
from matplotlib import rc
import scipy.stats as stats2) 함수 제작
- stats.beta : 베타분포 객체 생성(링크)
- stats.bernoulli.rvs(0.5, size = inp[-1]) : 베르누이 시뮬레이션(확률 0.5로 계산, inp[-1]로 지정한 것은 리스트(숫자가 커지는 형태)로 받아서 돌릴때 가장 마지막 값(가장 긴 값)을 근거해서 그림을 그릴 것이기 때문)
- dist.pdf(x, 1 + heads, 1+ N - heads) : 각 x에 대한 확률밀도를 계산
- plt.fill_between : 차트 내부 채우기
def coin(inp):
dist = stats.beta
len_inp = len(inp)
data = stats.bernoulli.rvs(0.5, size = inp[-1])
x = np.linspace(0, 1, 100)
size_y = 5 * len_inp
fig = plt.figure()
fig.set_size_inches(15, size_y)
rc('font', family='AppleGothic')
for k, N in enumerate(inp):
sx = fig.add_subplot(len_inp, 1, k+1)
plt.xlabel("$p$, 앞면의 확률", fontsize = 13)
plt.setp(sx.get_yticklabels(), visible=False) # ylabel 생략
heads = data[:N].sum()
y = dist.pdf(x, 1 + heads, 1 + N - heads)
plt.plot(x, y, label = "%d 번의 동전 던지기, \n앞면 %d 번 관측" % (N, heads))
plt.fill_between(x, 0, y, color = "#348ABD", alpha = 0.4)
plt.vlines(0.5, 0, 4, color = "k", linestyles = "--", lw = 1)
leg = plt.legend()
leg.get_frame().set_alpha(0.4)
plt.autoscale(tight = True)
plt.suptitle("사후확률의 베이지안 업데이트", y=1.02, fontsize = 14)
plt.tight_layout()2. 결과
n_trials = [0, 1, 2, 3, 4, 5,8, 15, 50, 500]
coin(n_trials)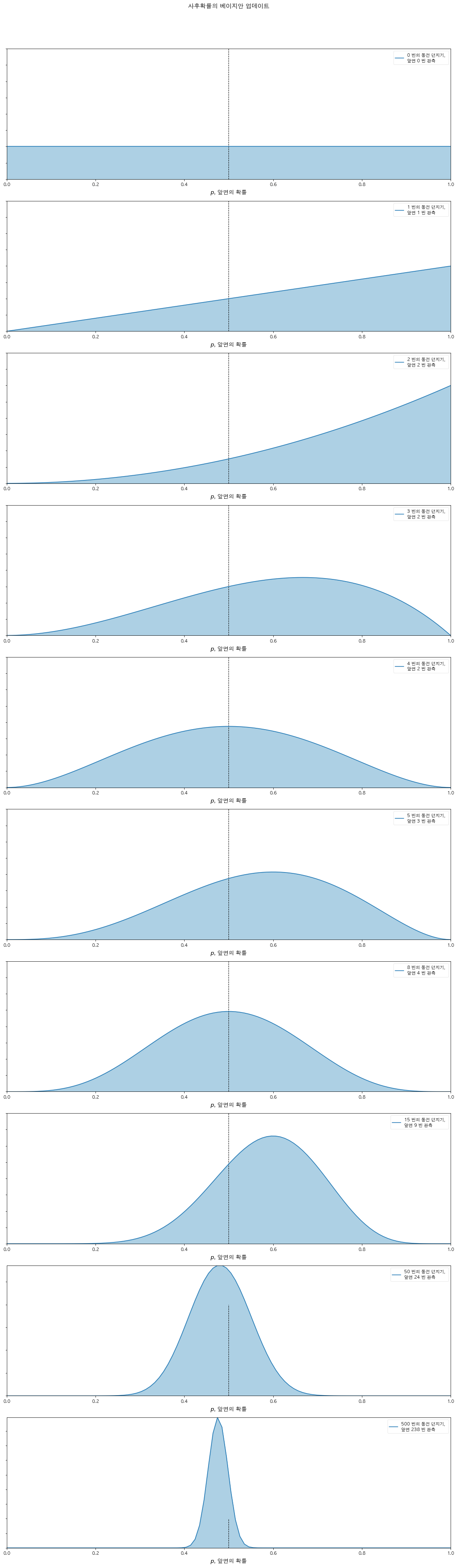
3. 참고
- rv.rvs
- 베타분포
- 코드원본
- 프로그래머를 위한 베이지안 with 파이썬(캐머런 데이비슨 필론)
'Science > 통계학' 카테고리의 다른 글
| [통계학] python을 이용한 귀무가설의 판정 (0) | 2020.09.09 |
|---|---|
| [통계학] PYTHON을 이용한 U 값 계산 (0) | 2020.09.03 |
| [통계학] 몬테 카를로 방법을 통한 원의 넓이 계산(python) (0) | 2020.08.30 |
| [통계학] python을 이용한 블로그 방문자수 회귀선 그리기 (0) | 2020.08.29 |
| [통계학] python을 이용한 부트스트랩 구현 (2) | 2020.08.28 |
Comments



